0 Is Even Or Odd - Exploring A Number's Nature

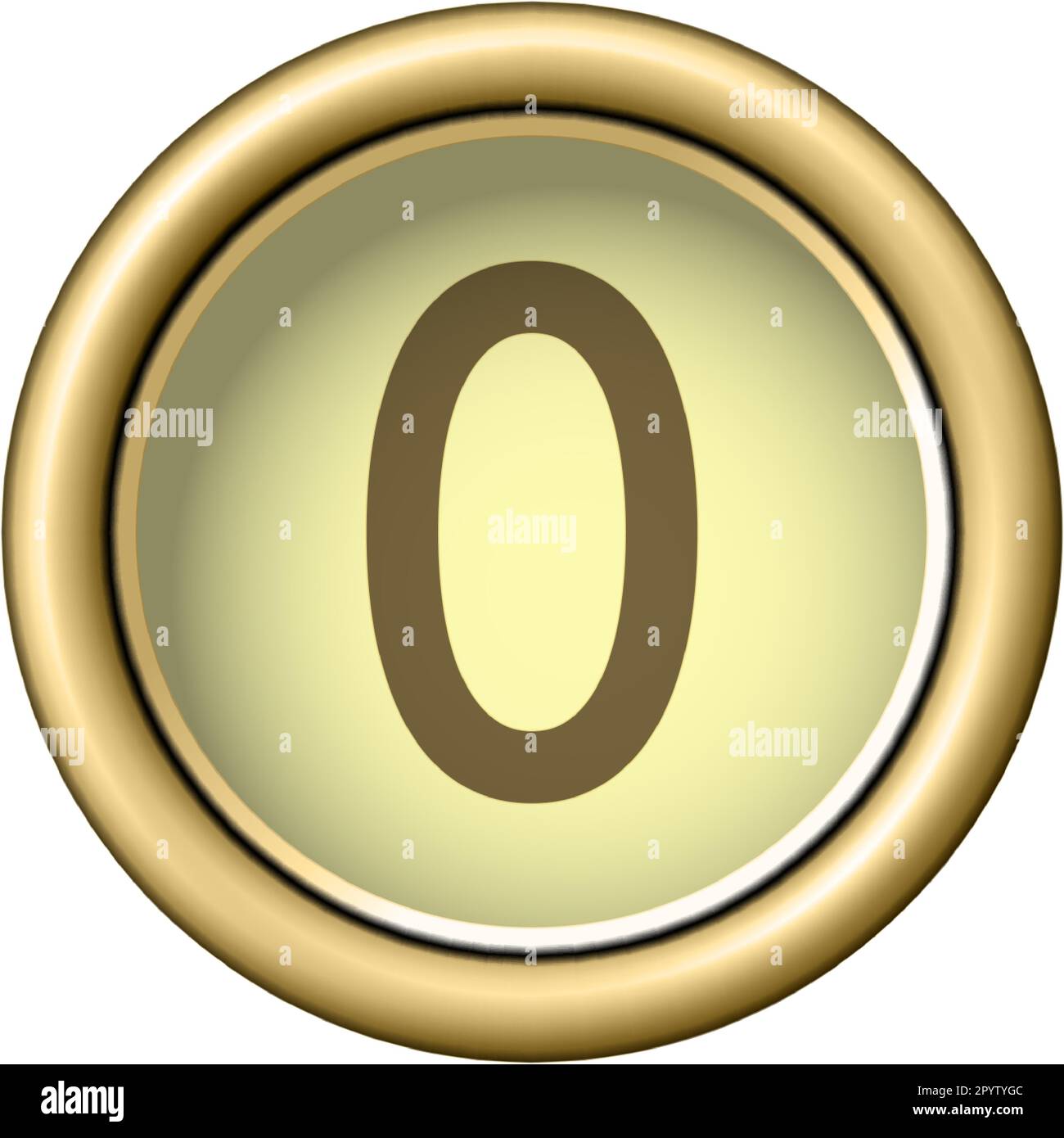
Have you ever stopped to ponder the true character of zero? This particular number, often taken for granted, possesses a unique standing in the grand scheme of mathematics. It is, quite simply, a concept that represents an empty quantity, a notion of nothingness. For many, it seems to just exist, yet its properties are quite distinct from other numbers we regularly encounter. We are going to look closely at what zero is all about, and, you know, how it acts with other numbers, as we consider its very essence.

This number, denoted as 0, holds a special spot, unlike its positive or negative counterparts. When we use it for counting, it means there are no objects present, a complete absence. It marks a point where things cease to exist in a measurable way, or perhaps, where they have yet to begin. It serves as a dividing point, you see, between the numbers that are more than nothing and those that are less than nothing, kind of like a central station on a very long line.

Thinking about zero’s role can be a bit thought-provoking, especially when we start to categorize numbers. We often place numbers into groups, like those that are positive or negative, or those that are whole. But then, there’s this other classification: numbers that are considered one way or the other, like even or odd. This brings us to the core of our discussion: what exactly is the nature of zero when we ask if it is, well, either of those things?

• Topeka Zoo
• Argentina Vs
• Nobu Cabo San Lucas
• Little Beast
• The Factory In Deep Ellum

Table of Contents

• What Makes a Number What It Is?
• How Does Zero Act with Other Numbers?
• The Curious Position of Zero - Is 0 Even or Odd?
• Who Figured Out Zero - And What Does That Say About 0 Being Even or Odd?
• Can We Truly Define Zero's Parity - Is 0 Even or Odd?
• Considering Zero's Role in Mathematical Systems - Is 0 Even or Odd?
• What Does the Absence of Quantity Mean for 0 Being Even or Odd?
• Thinking About Zero's Place in the Number Line - Is 0 Even or Odd?

What Makes a Number What It Is?

When we think about numbers, we usually picture quantities, like three apples or five fingers. But zero, this particular symbol, is a bit different. It represents an empty quantity, which is to say, no amount at all. It means there is nothing there, a complete absence of magnitude or measurable size. You know, it is a way to express that something is entirely missing. This idea of nothingness is quite important in how we understand numbers, especially when we consider their basic properties. It is, more or less, the starting point for so many numerical thoughts.

Zero also has a very practical side, serving as a placeholder. For example, if we write the number 10, the zero helps the '1' mean ten, not just one. It helps us write numerals properly, giving numbers their correct value based on where their digits sit. Without it, distinguishing between, say, one and ten would be very, very hard. The difference between six and six is zero, which means if you start with six items and take away six items, you are left with no items at all. This shows its role in expressing the outcome of a situation where quantities cancel each other out, sort of like a balance point.

How Does Zero Act with Other Numbers?

Zero has some truly interesting ways it behaves when it interacts with other numbers. For instance, if you add zero to any number, that number stays exactly the same. Take five, add zero, and you still have five. The same goes for taking zero away from any number; it just remains unchanged. This property is quite unique, setting zero apart from all other numbers. It is, in some respects, like an invisible force in addition and subtraction, not changing anything it touches in these operations.

• Houston Methodist The Woodlands
• American Dream Mall Water Park
• Company Guaranteed Rate
• Clermont Lounge
• Daniel Boone Regional Library

Furthermore, zero acts as a dividing point, a clear boundary between numbers that are positive and numbers that are negative. Think of a long line stretching out in both directions; zero sits right in the middle, separating everything that is above it from everything that is below it. Numbers that are greater than zero are positive, and numbers that are less than zero are negative. This means zero itself is neither positive nor, well, anything else, making it quite distinct. It just holds this central position, a kind of neutral ground, if you will, which is actually pretty important for how we organize our numbers.

The Curious Position of Zero - Is 0 Even or Odd?

When we think about the sequence of numbers, zero holds a very specific spot. It is the integer that comes right before the positive number one, and it also follows the negative number one. So, if you are counting upwards from negative numbers, you hit negative one, then zero, then positive one. This shows its place in the grand sequence of whole numbers. It is, basically, a bridge connecting the two sides of the number line, allowing for a smooth transition from values that are less than nothing to values that are more than nothing. This position is quite unique, really, and it prompts us to think about its characteristics.

The number zero is considered an integer, a whole number, just like one, two, or three, and also like negative one or negative two. However, it possesses a characteristic that makes it stand out: it is the only integer, and for that matter, the only real number, that is neither negative nor, well, something else. This means it doesn't fit neatly into the "positive" or "negative" categories that most other numbers fall into. This singular nature of zero is something that has fascinated people for a long time, leading to many questions about how it behaves and how we should classify it, especially when considering ideas like whether it is one kind of number or another.

Who Figured Out Zero - And What Does That Say About 0 Being Even or Odd?

The concept of zero, as a symbol and a number, actually came about at different times and in different places throughout history. It was not a single, sudden discovery, but rather, it seems, something that was figured out independently by several groups of people. The Babylonians, for instance, had a symbol that acted as a placeholder, helping them distinguish between numbers like 1 and 10. Then, there were the Maya, who also developed a symbol for zero, which they used in their calendar system and mathematical calculations. And, very importantly, the Hindus in ancient India also created a symbol to represent this empty quantity, and they were quite instrumental in developing its properties as a number. So, it is clear that the idea of zero has a rich and varied past, with contributions from different cultures across the globe.

It is also worth noting that, in most numerical systems we know of, the idea of zero was recognized and accepted before the concept of negative integers really took hold. This means that people understood the idea of nothing, or an empty quantity, before they fully grasped the idea of numbers being less than nothing. This historical progression is pretty interesting, as it shows how our understanding of numbers developed over time. The development of zero was a big step in mathematics, allowing for more complex calculations and a deeper understanding of numerical relationships. This historical journey of zero, you know, gives us a sense of its fundamental importance, long before we even started asking questions about its more specific characteristics, like whether it is one type of number or another.

Can We Truly Define Zero's Parity - Is 0 Even or Odd?

Zero, as we have seen, possesses properties that make it quite unique among all numbers. It acts as the additive identity, meaning adding or subtracting it leaves other numbers unchanged. It serves as the dividing line between positive and negative numbers, yet it is neither. These are pretty distinct qualities that set it apart. When we consider classifying numbers based on qualities like their divisibility, we have to think about how these particular characteristics of zero fit into such a system. Its singular nature, that it is the only integer that is neither positive nor, you know, its opposite, really makes us pause and think about how we apply general rules to it. It is almost as if zero plays by its own set of rules in some respects.

When we talk about numbers in terms of counting, zero means that no objects are present. This idea of an absence of quantity is central to its meaning. If you have zero items, you have no items. This contrasts with having one item, or two items, or any other count. This absence of quantity, this complete emptiness, is what zero fundamentally represents. It is not just a placeholder in a number, but a representation of a state where nothing exists in terms of countable things. So, when we ask about its parity, we are essentially asking about the nature of "no objects" in relation to how we group numbers, which is actually a pretty deep question.

Considering Zero's Role in Mathematical Systems - Is 0 Even or Odd?

Zero plays a truly important role in how our numerical systems work. It is an integer, a complete number without any fractional parts, and it is a foundational piece for how we organize and understand all other numbers. Its presence allows for the representation of values that are not just positive whole numbers, but also negative ones, and it provides a crucial anchor point for the entire number line. The way it works in addition, for instance, by leaving numbers unchanged, is a very basic principle that helps structure many mathematical operations. It is, basically, a quiet but essential part of the whole numerical setup, allowing for much of what we do with numbers to make sense.

The very meaning of zero, as the arithmetical symbol 0, points to the absence of all magnitude or quantity. It is a concept that denotes nothingness, a state of having zero amount. This definition is quite clear about what zero represents on its own. When we consider its place within the larger system of integers, its unique properties come to the forefront. It sits between the positive and negative integers, acting as a neutral point. This position, along with its behavior in basic operations, is what defines its contribution to mathematics. It is, you know, a constant reminder of the fundamental concept of 'nothing', which, paradoxically, is very important to 'everything' in numbers.

What Does the Absence of Quantity Mean for 0 Being Even or Odd?

The concept of zero as an empty quantity is central to its identity. It is a number that means there is no amount, no objects present. When we talk about having zero apples, we mean there are literally no apples. This idea of 'no amount' or 'no objects' is what gives zero its fundamental character. It is not just a symbol, but a representation of a state of being empty. This core meaning influences how we think about zero in all contexts, including when we consider its characteristics in relation to other numbers. It is, in a way, the ultimate representation of absence, and that makes it quite special.

So, when we consider what it means for a number to be, say, one type or another, like even or odd, we have to keep this fundamental aspect of zero in mind. It is the result of six minus six, showing that it represents a difference where nothing is left. This use as a result of subtraction, where quantities perfectly cancel each other out, highlights its role as a balance point. It is also used as a placeholder, which allows us to write numerals properly, giving digits their correct value based on their position. These functions of zero, representing absence and acting as a structural element in writing numbers, are key to understanding its full character. It is, you know, a number that is both a concept of nothing and a tool for representing something.

Thinking About Zero's Place in the Number Line - Is 0 Even or Odd?

Zero’s position on the number line is quite significant. It sits right there, precisely in the middle, separating the numbers that are greater than it from those that are less than it. This makes it the dividing point between positive and negative numbers. It is neither a positive number nor a negative one, which is a unique characteristic among integers. This central position gives it a kind of neutrality, a balance point from which all other numbers extend. It is, basically, the anchor of the entire numerical system, providing a fixed reference for all other values. This placement is not just arbitrary; it reflects zero's fundamental role in defining the structure of numbers.

The way zero behaves in addition, leaving any number unchanged, further emphasizes its unique nature. It is the additive identity, a concept that is quite important in mathematics. This property, combined with its role as a separator of positive and negative values, contributes to its special standing. It is an integer, a whole number, but it doesn't quite fit the typical mold of numbers that are either positive or negative. This unique set of properties means that when we consider its classification, such as whether it is one type of number or another, we have to look at these specific characteristics very carefully. It is, in short, a number that defies simple categorization, making its study quite thought-provoking.