Is 0 An Even Number - Unpacking A Common Question

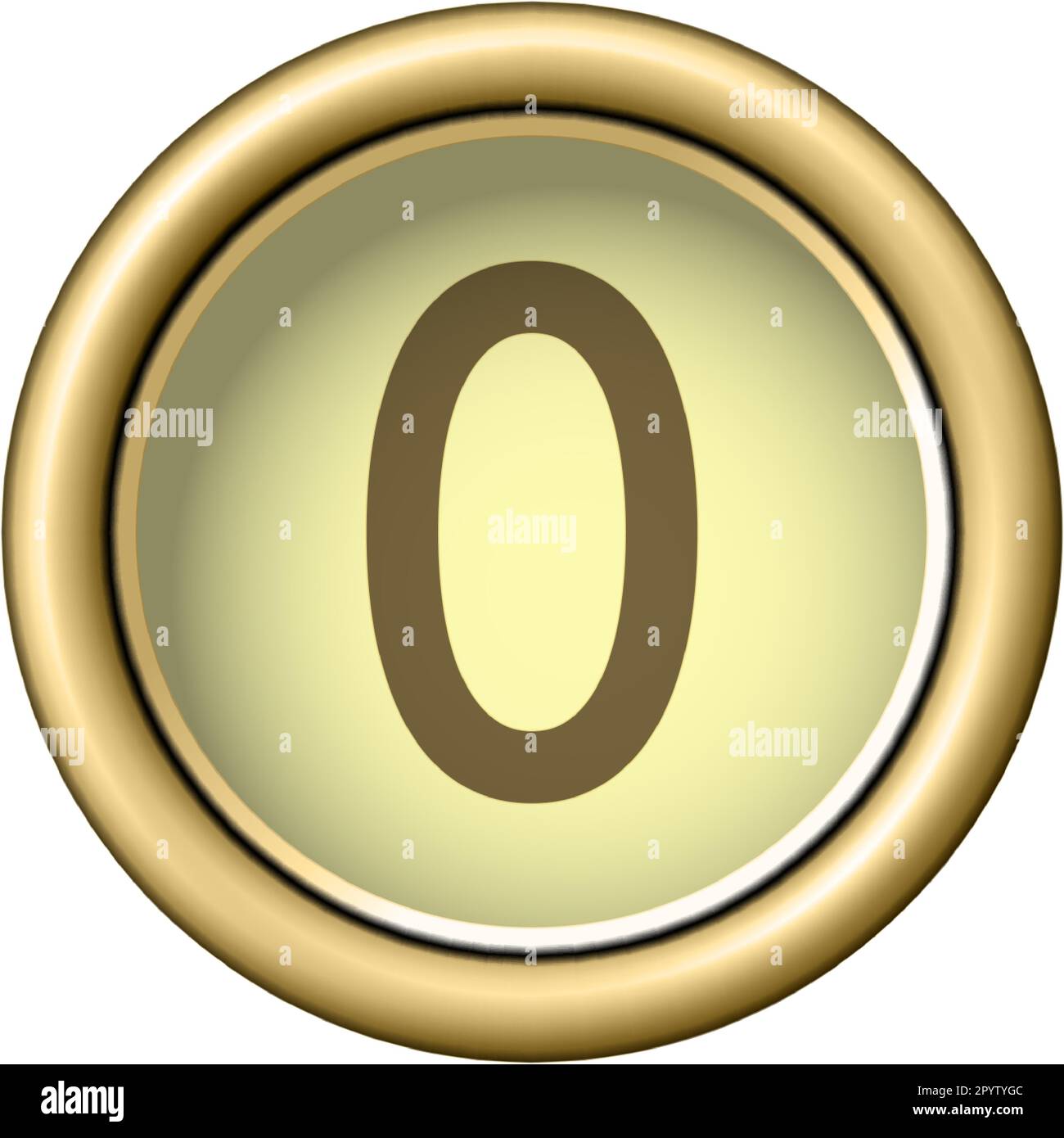
Have you ever paused to think about the number zero? It seems so simple, just a placeholder, but it holds a few interesting surprises. One of the most talked-about questions concerning this humble digit often pops up in conversations, sometimes even sparking a bit of friendly debate. People frequently wonder if zero, that neutral spot on the number line, actually counts as an even number.

It's a really good question, honestly, and one that makes a lot of sense to ask. For many, the idea of even numbers usually brings to mind things like two, four, six, and so on. Odd numbers are usually one, three, five, and their companions. Zero, however, doesn't quite fit neatly into those typical groups in everyone's mind, making its true nature a little bit fuzzy for some.

Yet, the answer, as we'll see, is pretty straightforward once you look at how numbers are generally defined. This isn't just a matter of opinion; there's a clear, accepted way of looking at it within the broader world of numbers. We'll explore why zero absolutely belongs in the group of even numbers and why this particular piece of information is, in fact, quite helpful in many situations, too it's almost.

• Clermont Lounge
• Wharton Center Cobb Great Hall East Lansing Mi
• Little Beast
• Sheepshead Bay Regal Cinema
• Oregon Zoo Tickets

Table of Contents

• The Question of Zero's Parity - Is 0 an Even Number?
• Why Zero Fits the Even Definition - Is 0 an Even Number Clearly?
• Zero's Behavior with Other Numbers - Is 0 an Even Number in Action?
• The Alternating Pattern - Where Does 0 Sit, Is 0 an Even Number?
• Common Misconceptions - Why Some Doubt, Is 0 an Even Number?
• The Mathematical Community's View - Is 0 an Even Number, Generally Accepted?
• Practical Uses of Zero's Parity - How is 0 an Even Number Useful?
• Beyond Simple Counting - Why Understanding Is 0 an Even Number Matters?

The Question of Zero's Parity - Is 0 an Even Number?

When we talk about numbers being "even" or "odd," we're really talking about their parity. This quality tells us whether a whole number can be split into two equal groups without anything left over. For most numbers, this is a pretty simple idea. You can split six into two groups of three, so six is even. You can't split five into two equal whole number groups, so five is odd. But what about zero? That's the part that sometimes causes a bit of head-scratching, you know.

The basic idea behind an even number is that it can be divided by two and result in another whole number. So, if you take any number and cut it in half, and that half is a number without any fractions or decimals, then the original number is even. This is the simple, honest way we look at it. Zero, it seems, fits this description perfectly, which is pretty cool.

Consider this: if you have zero cookies, and you want to share them equally between two people, how many cookies does each person get? They each get zero cookies. Zero divided by two is zero, and zero is definitely a whole number. This simple thought experiment, actually, helps clear up a lot of the confusion people sometimes have about this particular number's status.

• Regal Springfield Town Center
• Fogo De Chao Atlanta
• High Country Gardens
• Evo San Marcos
• Fogo De Chao Boston

Why Zero Fits the Even Definition - Is 0 an Even Number Clearly?

The standard way we define an even number is that it's an integer that is a multiple of two. This means you can write it as 2 times some other integer. For example, four is 2 times 2. Ten is 2 times 5. So, if we apply this same rule to zero, what do we find? Zero can be written as 2 times 0. Since zero itself is an integer, zero perfectly matches the requirement for being an even number. This definition is very widely accepted by people who study numbers.

You might recall from a source, perhaps something you've read online, that the number zero is indeed described as even. This isn't just a random idea; it's based on how numbers work and how they relate to each other. The way zero behaves with other numbers, and its place in the sequence of numbers, all point to it being an even one. It's a rather simple truth once you look at the established rules, too it's almost.

Think about it this way: if a number is even, it means it leaves no remainder when you divide it by two. Zero, when divided by two, leaves no remainder. The result is zero. This straightforward test confirms its even nature. There's no real wiggle room here when you stick to the mathematical rules. It's just how it works, as a matter of fact.

Zero's Behavior with Other Numbers - Is 0 an Even Number in Action?

Numbers interact with each other in predictable ways, and zero is no exception. When you add two even numbers, the result is always even. For instance, two plus four gives you six, which is even. When you add two odd numbers, the result is also even. Take three plus five, and you get eight, which is even. Now, what happens if you add an even number and an odd number? The result is always odd. Two plus three makes five, an odd number.

Let's see how zero fits into these patterns. If zero is truly an even number, then adding it to another even number should give an even result. Zero plus four equals four, which is even. This works out. If you add zero to an odd number, like zero plus five, you get five, which is odd. This also works perfectly, which is pretty neat. The way zero behaves in addition and subtraction clearly shows its even characteristics, you know.

Consider multiplication, too. A source you might have seen points out that an even number multiplied by an odd number always results in an even number. For example, two multiplied by three gives you six, which is even. If zero is even, then zero multiplied by any odd number should give an even result. Zero times three is zero, and zero is even. This pattern holds true, which is quite telling. The number zero, in these interactions, acts just like any other even number, actually.

The Alternating Pattern - Where Does 0 Sit, Is 0 an Even Number?

If you look at the number line, numbers alternate between odd and even. You have..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ... This pattern is pretty consistent. If you move from an odd number to the next whole number, you get an even one. If you move from an even number to the next, you get an odd one. So, if we follow this sequence, where does zero fall?

Right before zero, you have negative one, which is odd. Right after zero, you have one, which is also odd. For the pattern to hold, the number between two odd numbers must be even. Therefore, zero must be an even number to keep this natural rhythm going. It just makes sense, doesn't it? The flow of numbers on the line truly supports this idea, in a way.

This alternating nature is a fundamental aspect of how numbers are structured. If zero were considered odd, or neither, it would break this very consistent and useful pattern. The mathematical world prefers things to be orderly and predictable, and zero being even helps maintain that order. It's a rather elegant fit, honestly, into the larger system of numbers.

Common Misconceptions - Why Some Doubt, Is 0 an Even Number?

It's common for people to feel a bit unsure about zero's parity. One reason for this doubt might be that zero is often seen as "nothing" or "neutral." It doesn't have a positive or negative sign, and it doesn't represent a quantity in the same way that two or five do. This unique quality can make it seem like it stands apart from other numbers, making its classification a little less obvious at first glance. People sometimes think of even numbers as being "positive" even numbers, which is not the full picture, you know.

Another reason for confusion could be that some people learn about even numbers starting from two, four, six, and so on, without explicitly including zero. This can lead to an incomplete idea of what an even number truly is. If the initial teaching doesn't clearly state that zero is even, it's pretty natural for someone to question it later on. It's just a matter of how we're introduced to these concepts, basically.

Also, in some everyday contexts, the concept of "even" might imply divisibility into two *non-zero* parts, or perhaps something that can be physically paired up. Since zero items can't be physically paired, this informal idea might lead to confusion. However, in mathematics, the definition is much more precise and doesn't rely on physical representation. It relies on the ability to be expressed as two times an integer, which zero certainly can, as a matter of fact.

The Mathematical Community's View - Is 0 an Even Number, Generally Accepted?

Within the community of people who work with numbers, there's really no debate about zero's parity. It's widely accepted that zero is an even number. This consensus comes from the consistent application of definitions and the way zero behaves within mathematical systems. If you ask someone who studies numbers, they will almost certainly tell you that zero is even, and they can usually explain why using the standard definitions.

The definition of an even number, as a multiple of two, is a fundamental concept. Because zero fits this definition without any exceptions or special rules, it's simply included in the set of even numbers. There's no need for a separate category or an asterisk next to its name. It's just part of the group, which is pretty straightforward. This is how the system maintains its consistency, you know.

This acceptance isn't just about sticking to rules; it's about maintaining a logical and coherent system. If zero were considered odd, or neither, it would cause inconsistencies in many mathematical properties and patterns. For instance, the alternating sequence of odd and even numbers would break. So, for the sake of mathematical harmony, zero is, and has been for a very long time, considered an even number. It's a foundational piece of how numbers work, basically.

Practical Uses of Zero's Parity - How is 0 an Even Number Useful?

Knowing that zero is an even number isn't just a piece of trivia; it's actually quite useful in many areas. For example, when creating formulas or solving puzzles that involve number patterns, treating zero as an even number helps these formulas work correctly across all integers. If you're building a system that relies on the parity of numbers, and you don't account for zero properly, your system might have unexpected hiccups, you know.

One source points out that it's quite helpful to treat zero as an even number, especially for patterns and puzzles. If someone is developing a formula that works for something and uses the parity of numbers, making sure zero is correctly identified as even ensures the formula remains accurate and reliable. This means fewer special cases or exceptions to worry about, which simplifies things quite a bit, honestly.

Think about computer programming, too. While some of the source material touches on how zero is used in other technical ways, like for network addresses or as a "null pointer constant," its mathematical parity is still important when dealing with numerical operations. If a program needs to process a list of numbers and sort them based on whether they're even or odd, zero needs to be correctly categorized for the program to function as expected. It's a subtle but important detail, as a matter of fact.

Beyond Simple Counting - Why Understanding Is 0 an Even Number Matters?

Understanding zero's parity goes a little beyond just knowing if it's even or odd. It helps us appreciate the careful way mathematical definitions are built. These definitions aren't just made up; they are created to be consistent and to make sense across the entire number system. When we see that zero fits neatly into the definition of an even number, it shows how logical and well-structured mathematics truly is, you know.

This topic also highlights how everyday language and common intuition can sometimes differ from precise mathematical definitions. What might seem like a simple question about a number can actually reveal deeper principles about how numbers are categorized and how they behave. It encourages a more precise way of thinking, which is valuable in many different fields, honestly.

Ultimately, recognizing zero as an even number helps us maintain a consistent and complete picture of the number line. It ensures that rules about even and odd numbers apply universally, without needing to create special exceptions just for zero. This consistency makes mathematics a more powerful and predictable tool, which is pretty cool. It really is a key piece of the number puzzle, basically.